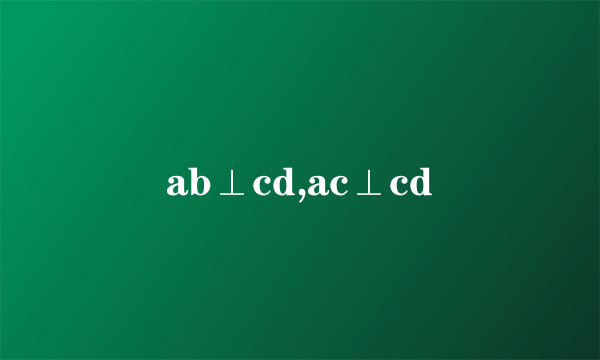
证明:
1.过A作AH⊥平面BCD于H,则AH⊥CD
又∵AB⊥CD,AB与AH交于A
∴CD⊥平面ABH
∴CD⊥BH
同理BD⊥CH
∴在三角形BCD中H为垂心
∴BC⊥DH
又∵AH⊥BC,DH与AH交于H
∴BC⊥平面ADH
∴点A在面BCD上的射影H为△BCD的垂心
2.
AD*BC=(AC+CD)*(BA+AC)
=AC*BA+AC*AC+CD*BA+CD*AC
=AC*BA+AC*AC+CD*AC
=AC*(BA+AC+CD)
=AC*BD
=0
所以AD⊥BC
标签:cd,ab,ac
版权声明:文章由 百问十四 整理收集,来源于互联网或者用户投稿,如有侵权,请联系我们,我们会立即处理。如转载请保留本文链接:https://www.baiwen14.com/life/154339.html





















